NMT：阿里联合加州大学伯克利分校推出的多任务学习框架

NMT简介

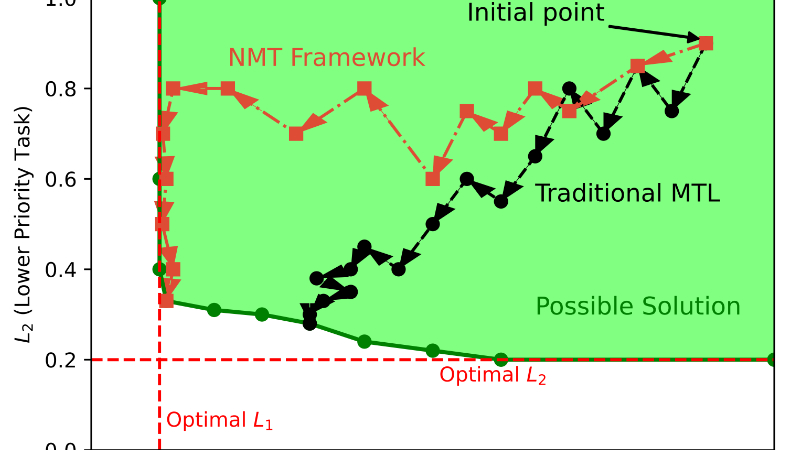
No More Tuning（NMT）是由加州大学伯克利分校和阿里巴巴集团共同开发的一种创新的多任务学习框架。该框架采用拉格朗日微分乘数法，通过将多任务学习问题转化为约束优化问题，优先优化高优先级任务的性能，同时确保低优先级任务的优化不会对其产生干扰。NMT框架的核心优势在于其无需手动调整超参数，通过直接将任务优先级嵌入到优化问题的约束中，简化了模型训练过程，降低了复杂性和时间消耗。此外，NMT还提供了理论分析，确保了高优先级任务的性能优化，并且可以轻松集成到现有的基于梯度下降的多任务学习方法中。在多个公共数据集和大规模工业系统中的实验验证了其在不同领域和应用中的广泛适用性和有效性，展示了其在提升高优先级任务性能的同时，保持其他任务稳定性能的能力.

NMT主要功能

• 优先级任务优化：能够优先优化高优先级任务的性能，确保其在多任务学习过程中不受低优先级任务的干扰，从而提升关键任务的性能表现.
• 无需手动调参：消除了传统多任务学习中需要手动调整任务权重参数的步骤，简化了模型训练过程，降低了调参的复杂性和时间消耗.
• 易于集成与扩展：可以轻松集成到现有的基于梯度下降的多任务学习方法中，无需对原有框架进行大规模修改，具有良好的兼容性和扩展性.
• 理论性能保证：提供了理论分析，确保在优化过程中高优先级任务的性能不会下降，增强了模型优化的可靠性和稳定性.
• 多任务平衡：在提升高优先级任务性能的同时，能够保持其他低优先级任务的稳定性能，实现多任务之间的有效平衡，避免因过度优化某一任务而导致其他任务性能下降.

NMT技术原理

• 约束优化问题：将多任务学习问题转化为约束优化问题，以高优先级任务的性能作为不等式约束条件，在优化低优先级任务时保持高优先级任务的性能不低于其最优值.
• 拉格朗日乘数法：利用拉格朗日乘数法将约束优化问题转化为无约束优化问题，通过引入拉格朗日乘数将约束条件融入到目标函数中，从而可以使用梯度下降等优化算法进行求解.
• 分步优化策略：按照任务优先级顺序依次进行优化，首先优化最高优先级任务，找到其最优解，然后在保持高优先级任务性能不变的前提下，依次优化后续的低优先级任务.
• 梯度下降与上升：在优化过程中，对模型参数θ采用梯度下降算法进行更新，以最小化目标函数；同时对拉格朗日乘数λ采用梯度上升算法进行更新，以满足约束条件的最大化要求.
• 重缩放损失函数：为了避免在拉格朗日乘数λ较大时损失函数过大导致参数更新不稳定，对损失函数进行重缩放处理，确保每个损失的组合是一个标准化的凸组合，从而保持优化过程的稳定性.

NMT应用场景

1. 推荐系统：在电商、视频平台等推荐系统中，NMT可以同时优化多个目标，如用户点击率（高优先级）、用户停留时长、广告收益等，确保在提升核心用户体验的同时，兼顾其他业务指标.
2. 搜索引擎：在网页搜索、商品搜索等搜索引擎中，NMT可以优先优化搜索结果的相关性（高优先级），同时考虑点击率、用户满意度等其他指标，提高搜索质量和用户体验.
3. 金融风控：在金融风险控制领域，NMT可以同时考虑多个风险评估指标，如违约率（高优先级）、逾期率、坏账率等，确保在严格控制核心风险的同时，平衡其他风险因素.
4. 医疗诊断：在医疗诊断系统中，NMT可以优先优化诊断准确性（高优先级），同时考虑诊断速度、误诊率等其他指标，提高医疗诊断的综合性能.
5. 自动驾驶：在自动驾驶系统中，NMT可以同时优化多个行驶目标，如安全性（高优先级）、行驶效率、能耗等，确保在保障行车安全的前提下，提升驾驶体验和系统性能.
6. 智能制造：在智能制造领域，NMT可以用于优化生产过程中的多个目标，如产品质量（高优先级）、生产效率、成本控制等，实现生产过程的智能化和精细化管理.

NMT项目入口

• arXiv技术论文：https://arxiv.org/pdf/2412.12092